| Everyone needs a Highly Reliable product, but How does one verify the reliability? One of the parameters that measures the reliability is MTBF. |
|
| Reliability is the probability that a device will perform its expected function for a set time period. MTBF is the calculated average time it will take for a system to fail. As can be seen by these definitions, reliability and MTBF are items that are very important when deciding which products or devices a customer may purchase. These numbers can be very deceiving and also very difficult to calculate. This document is an attempt to present one of the standard approaches to estimate the MTBF and reliability of an electronic product. |
|
| The history of approach to reliability and some of the models used to analyse, calculate & test the reliability is given in APPENDIX-A. |
|
Terms and Their Meanings
|
| |
| Failures - The number of units which failed within the time period. |
|
| MTBF - Mean Time between Failures, is the average time between system failures of the entire sample population. It is calculated as the total time over the number of failures. |
|
| MTTF - Mean Time to Failure is similar to MTBF and is used for systems that are replaced upon failure. MTTF is calculated as total time divided by the number of units under test. |
|
MTBF Basics & Methodology
|
| |
| There are several methodologies by which MTBF can be calculated. One of most popular methodologies which is used to calculate MTBF in our computer on modules and camera boards is presented here. |
|
| A common unit used for failure rate is failures/million hours. This is simply the number of failures expected to have in a million hours of operation of the equipment. Failure rates for many basic devices are well below 1 failure per million hours, so these values may seem insignificant. MTBF, or Mean Time Between Failures, is the inverse of the failure rate and is the average time between failures. It is calculated from the failure rate as follows: |
|
MTBF = 1,000,000/Failure Rate
|
|
| But with hundreds of parts in a design and having thousands of systems operating in the field, the failure rates will quickly add up. The parts count method is a technique for developing an estimate or prediction of the average life, the Mean Time Between Failures (MTBF), of an assembly. It is a prediction process whereby a numerical estimate is made of the ability, with respect to failure, of a design to perform its intended function. Once the failure rate is determined, MTBF is easily calculated as the inverse of the failure rate, as follows: |
|
System MTBF = 1 /
FR1 + FR2 + FR3 + ...........FRn
|
|
| where FR is the failure rate of each component of the system up to n, all components |
|
| The general procedure for determining a board level (or system level) failure rate is to sum individual failure rates for each component. For MIL-HDBK-217 based MTBF estimation, the summation is then added to a failure rate for the circuit board, which includes the solder joints. Component failure rates are provided by MIL-HDBK-217, "Military Handbook, Reliability Prediction of Electronic Equipment", as standard part failure rate models. The technology is being upgraded by manufacturer to improve the reliability of parts and hence manufacturer's data to is to be used wherever possible. |
| |
| The failure rates presented apply to equipment under normal operating conditions, i.e., with power on and performing its intended function in its intended environment. Consideration is to be given to various environments, component quality, and thermal aspects. A typical MTBF calculation example is given in APPENDIX-A. |
|
Conclusion
|
| |
| MTBF is really all about failure. Every product ever made will eventually fail, but ideally, not within its service life. MTBF calculations are used to determine the likelihood of failure. Many people will look at the MTBF of a product and make assumptions. For example, if an MTBF is 100000 hours, one may think they have a long time before having to replace their product. That is not the case but must go one step further. Given the MTBF, should calculate the reliability or the probability that it will last for as long as they intend to keep it in service. |
|
|
| Reliability Analysis, Life time estimation and Methods to increase the Product Reliability shall be continued in the Next Part of the article. |
|
APPENDIX - A [1]
|
|
1. HISTORY & PREDICTION MODELS
|
| |
|
The first approach to a reliability calculation system happened in Germany during WWII (about 1940) and involved the highly unreliable V-1 Rocket designed by Von Braun. German Mathematician, Eric Pieruschka, assisted Von Braun in coming up with the reliability calculation to describe the reasons for the failures. Prior to this time, mechanical reliability was approached as resolving the weakest link and that would solve the problem. That process did not work then, however, it only revealed more issues.
Mil-HDBK 217 - Military handbook published in 1965 defining a standard method to measure reliability used by the U.S. military. The two acceptable prediction processes under this standard are Parts Count prediction and Parts Stress prediction. This standard can be found in various active forms (software and hardware), the internet (in its last version - Mil- HDBK 217F) and by other organizations other than the military. Please note that newer devices etc may not be included in the tables outlining the expected failure rates etc.
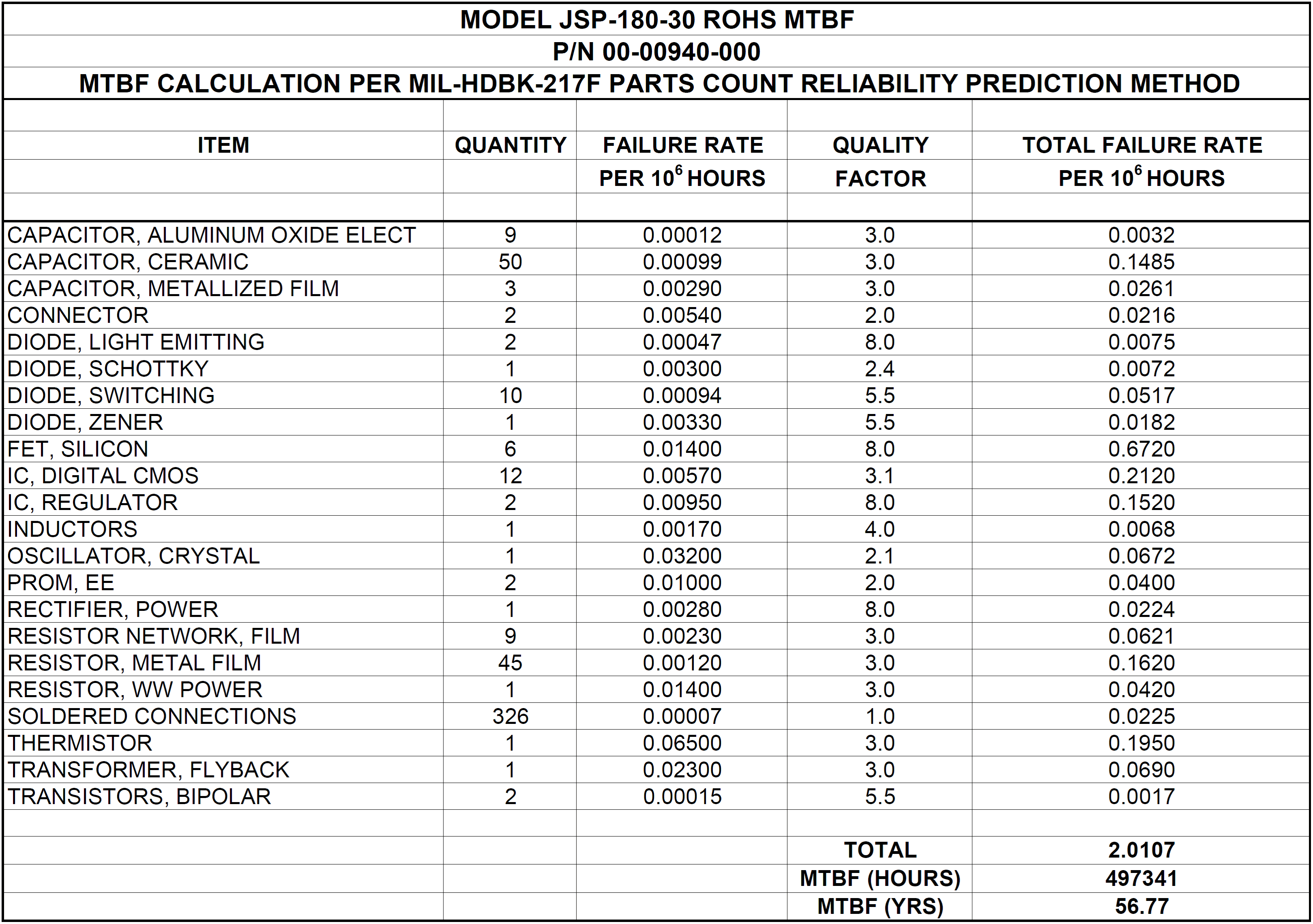
MTBF CALCULATION PER MIL-HDBK-217F PARTS COUNT PREDICTION METHOD
REFERENCES
[1] La Marche - Mean Time Between Failure (MTBF),by Vance Persons, Joseph Dykshorn RD02
|
|
 |