This guide explains how a stereo camera works and in turn aids in choosing the correct dimensions for a stereo camera for a target application. This guide only focuses on the geometrical treatment in the aim to keep the material short and simple. Other parameters that affect the design choices such as camera resolution, stereo technology, etc., will be explained in other blogs. If you have a quick query you can also email camerasolutions@e-consystems.com.
Before we dig into the details of the geometrical parameters that affect the stereo design the key term that one should understand is ‘disparity‘. The definition of disparity along with its illustration is provided in the following section.
What is Disparity?
Disparity is the difference in image pixel location of a particular 3D point when projected under perspective to two different cameras.
Disparity is usually denoted in terms of pixel shifts. The image shown below illustrates how pixels are shifted when a real-world scene is projected on to left and right cameras of a stereo camera.
Geometry of Projection in stereo
In an Ideal world, the Optic axes of 2 cameras are parallel. In the real world due to the lens distortion and errors in the manufacturing the Optic axes won’t be parallel and for that we need to perform camera calibration and use it for Stereo image rectification. The diagram below illustrates the ideal case in order to explain the effects baseline and focal length on depth measurements.
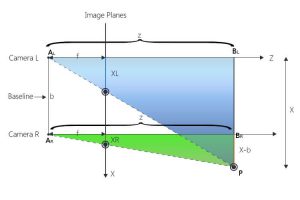
In the diagram above ‘f’ denotes the focal length of the stereo camera lenses, ‘b’ is the distance between the two centers of the left and right cameras (also called optical centers), ‘d’ is the disparity or pixel shifts. ‘Z’ is the distance of the 3D point ‘P’ intersecting the lines drawn from the optical centers.
With simple geometry we can derive ‘z’ as:
z=(b*f)/d
Where disparity d is equal to XL – XR, XL is the location of the real-world point P in the left image and XR is the location of the real-world point P in the right image.
In the above equation, depth ‘z’ is inversely proportional to disparity ‘d’ for a given point ‘p’. So ideally if a point is at infinity its disparity will be zero and we will not be able to identify the pixel shifts in left and right images. For closer objects the disparity is a big number.
‘z’ is directly proportional to the baseline distance (Tara supports baseline distance of 60mm) and focal length. So, if you choose a camera with longer baseline distance you should be able to cover longer distance, so is for the focal length. Also, it should be intuitive that choosing a longer baseline design but a shorter focal length lens (wide angle lens) cancels out the gain in achieving the distance.
So, an optimal tuning of these parameters – baseline distance and focal length is the first critical step in choosing a stereo camera for your target application. As mentioned in the beginning of this blog there are other parameters that need consideration to complete that design but is not covered in this blog.
As said earlier, disparity is denoted in pixel shifts and let’s assume we are scanning up to 128 pixels (stereo correspondence problem) to get the pixel shift for the point ‘p’ to calculate depth. In that case you will have 128 levels of depth. The following paragraph explains the distribution of these 128 levels of depth based on their corresponding disparity values.
Consider b = 6 cm , f = 450 pixels => b * f = 2700cm you will see Disparity Vs Depth map as shown below:
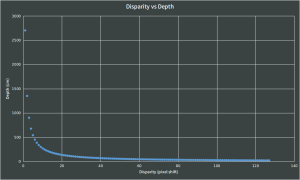
As you can see the depth points obtained are more concentrated and granular when they are in closer distances. For longer distances you will find sparse values and longer jumps. This means that your stereo camera precision is more reliable for reasonably closer objects and is less trustworthy for far away objects.
In conclusion, to increase Depth Range we can use factors like the baseline, focal length, resolution (Tara’s supports various resolutions) but you will start losing near depths. In order to compensate that we can further increase the disparity levels. If you increase the disparity levels the computation costs for stereo correspondence increase, so the problem becomes accuracy vs speed.
Tara’s accelerated SDK that runs on CUDA enabled GPU’s, solve the speed related problems. Write to us at camerasolutions@e-consystems.com to request early evaluation of the SDK.




