Ein umfassender Leitfaden zum Verständnis der Kameraprojektion und -Parameter

In der Welt der Bildverarbeitung und Kartierung basiert die Abbildung der 3D-Welt in eine 2D-Darstellung auf mathematischen Modellen, Transformationen und Kalibrierungsprozessen. Diese Prozesse werden durch Konzepte wie Kameraprojektion, intrinsische und extrinsische Parameter sowie Techniken zur präzisen Kalibrierung bestimmt. Das Verständnis dieser Prinzipien ist entscheidend für die Kamerakalibrierung und für Anwendungen wie autonome Fahrzeuge, Robotik und mehr.

In diesem Blog erhalten Sie fundierte Einblicke in diese Konzepte, indem wir die mathematischen Grundlagen und praktischen Anwendungen der Kameraprojektion aufschlüsseln.

Von 3D zu 2D: Das Konzept der Kameraprojektion

Im Kern umfasst die Kameraprojektion die Abbildung von 3D-Punkten der realen Welt auf eine 2D-Bildebene. Die Transformation wird häufig mithilfe des Pinhole-Kameramodells modelliert, das die Kamera als ein einfaches Gerät mit einer einzelnen Apertur betrachtet, durch die Licht eintritt.

Der Prozess lässt sich wie folgt zusammenfassen:

x=P.X

Hier:

• • x: 2D-Pixelkoordinaten auf der Bildebene
  • P: Die Kameraprojektionsmatrix (kapselt intrinsische und extrinsische Parameter)
  • X: 3D-Weltkoordinaten in homogener Form

Diese Transformation umfasst:

1. Extrinsische Transformation: Positioniert die Kamera relativ zur Szene durch Rotation und Translation der 3D-Punkte.
2. Intrinsische Transformation: Bildet diese transformierten Punkte mithilfe der internen Eigenschaften der Kamera auf die 2D-Bildebene ab.

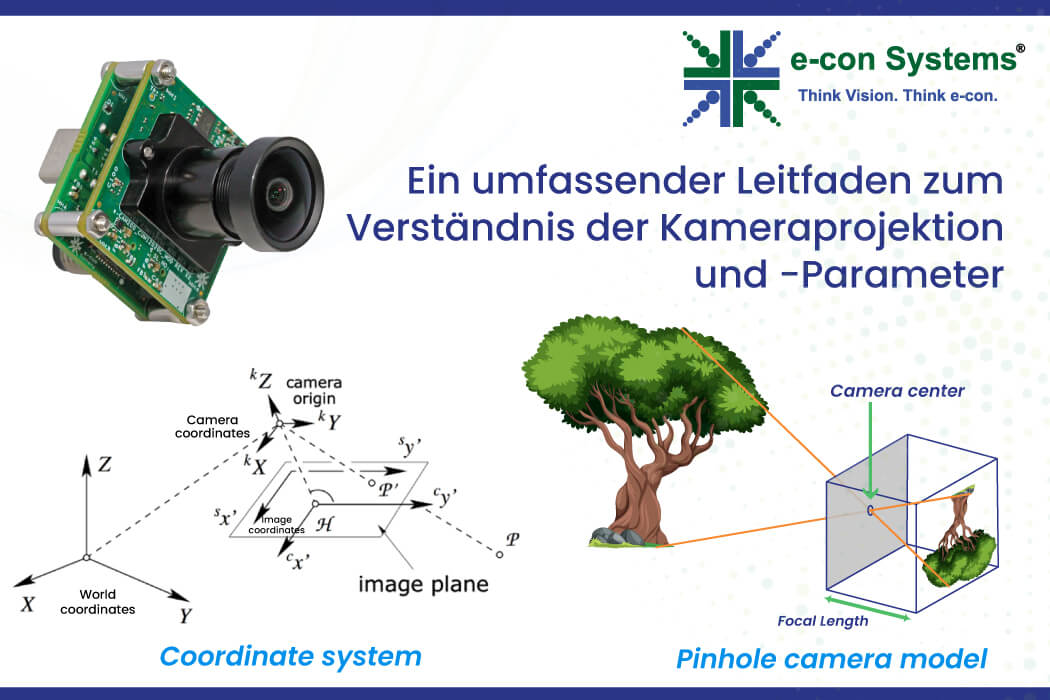
Koordinatensysteme in der Kameramodellierung

Der Weg eines 3D-Punkts zu seiner 2D-Darstellung erstreckt sich über mehrere Koordinatensysteme:

1. Weltkoordinatensystem: Definiert die 3D-Szene unter Verwendung eines globalen Referenzrahmens.
2. Kamerakoordinatensystem: Positioniert die Kamera als Ursprung, wobei die Welt relativ zu ihr transformiert wird.
3. Bildebene: Umfasst eine 2D-Ebene, auf die die Kamera die 3D-Punkte projiziert und die Szene erfasst.
4. Pixelkoordinatensystem: Repräsentiert das digitale Bild in diskreten Pixelwerten und verknüpft die Koordinaten der Bildebene mit tatsächlichen Pixeln.

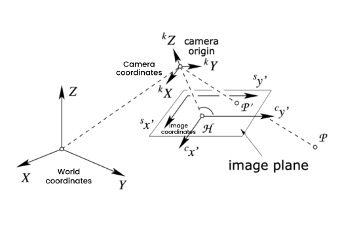Abbildung 1: Koordinatensysteme

Jede Transformation zwischen diesen Systemen wird durch intrinsische und extrinsische Parameter gesteuert.

Die Bausteine der Kameraprojektion

Intrinsische Parameter: Definition der internen Eigenschaften der Kamera

Intrinsische Parameter beschreiben die internen Eigenschaften einer Kamera und erfassen, wie sie 3D-Koordinaten im Kameraraum in 2D-Koordinaten auf der Bildebene transformiert. Dazu gehören:

• Brennweite (fx, fy): Repräsentiert den Abstand von der Linse zum Bildsensor und bestimmt den Maßstab der Projektion.
• Hauptpunkt (Cx, Cy): Das Zentrum der Bildebene, an dem die optische Achse schneidet.
• Seitenverhältnis und Scherung (s): Korrigiert Abweichungen von der Orthogonalität zwischen den Bildachsen.
• Verzerrungsparameter: Berücksichtigen Linsenverzerrungen wie Tonnenverzerrung (nach außen gekrümmt) oder Kissenverzerrung (nach innen gekrümmt).

Die intrinsische Matrix K fasst diese Parameter zusammen:

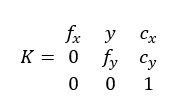
Extrinsische Parameter: Lokalisierung der Kamera im Raum

Diese Parameter definieren die relative Position und Orientierung der Kamera. Sie umfassen:

• Rotation (R): Eine 3×3-orthogonale Matrix, die die Orientierung der Kamera beschreibt.
• Translation (t): Ein 1×3-Spaltenvektor, der die Verschiebung der Kamera vom Ursprung angibt.

Kombiniert als:
[R|t]

Diese Parameter ermöglichen die nahtlose Integration der Kamera in eine 3D-Umgebung. Damit wird die Abbildung der 3D-Welt auf ein 2D-Bild vervollständigt.

Abbildung 2: Schachbrett – Punkterkennung [Image Source: pho1-22-Zhang-calibration.pptx ]

Kamerakalibrierung: Die Projektionsmatrix

Die Kalibrierung hilft dabei, die intrinsischen und extrinsischen Parameter zu bestimmen, um eine präzise Abbildung der 3D-Welt auf das 2D-Bild sicherzustellen.

Intrinsische Kalibrierung

Dieser Schritt konzentriert sich auf die Bestimmung von Parametern wie Brennweite, Hauptpunkt und Linsenverzerrung. Die Kalibrierung umfasst die Aufnahme von Bildern eines bekannten Musters (z. B. eines Schachbretts) und die Anwendung von Algorithmen wie der Methode nach Zhang zur Berechnung der Kameramatrix.

Extrinsische Kalibrierung

Hier besteht das Ziel darin, die Position und Orientierung der Kamera in der Szene zu schätzen. Durch die Zuordnung bekannter 3D-Weltpunkte zu ihren 2D-Projektionen können die extrinsischen Parameter abgeleitet werden.

Direct Linear Transform (DLT)

Die DLT-Methode ist der wichtigste Meilenstein der Kalibrierung und nutzt Korrespondenzen zwischen Weltpunkten und Bildpunkten. Sie formuliert Gleichungen für jede Korrespondenz und löst die Projektionsmatrix mithilfe linearer Algebra, beispielsweise durch QR-Faktorisierung.

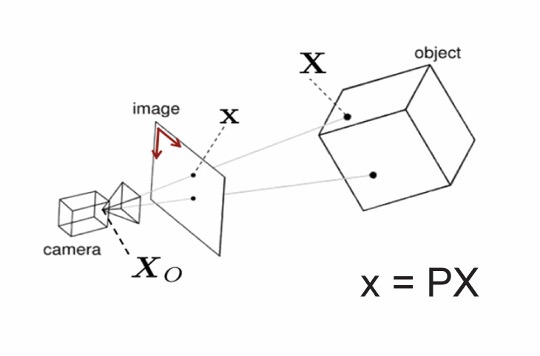Abbildung 3: Direct Linear Transform [Image Source: pho1-22-Zhang-calibration.pptx ]

Die Rolle des Pinhole-Kameramodells

Das Pinhole-Kameramodell vereinfacht den Projektionsprozess, indem es Linsenverzerrungen ignoriert und perfekte Optik annimmt. Obwohl idealisiert, bildet es die Grundlage für das Verständnis der Mathematik der Projektion.

In diesem Modell gilt:

• Lichtstrahlen konvergieren in einem einzigen Punkt (dem Pinhole) und treten zur Bildebene durch.
• Das resultierende Bild ist invertiert und skaliert, wobei die Skalierung durch die Brennweite bestimmt wird.

Reale Anwendungen erweitern dieses Modell häufig durch die Einführung von Verzerrungskorrekturen.

Linsenverzerrung und ihre Korrektur

Keine Linse ist perfekt, und Verzerrungen können die Bildqualität erheblich beeinträchtigen. Häufige Typen sind:

1. Radiale Verzerrung: Gerade Linien erscheinen gekrümmt
   • Tonnenverzerrung: Linien krümmen sich vom Zentrum nach außen
   • Kissenverzerrung: Linien krümmen sich nach innen

   

   Abbildung 4: Arten der Linsenverzerrung und deren Korrektur

2. Tangentiale Verzerrung: Entsteht durch Fehljustierung der Linse und verschiebt das Bild asymmetrisch

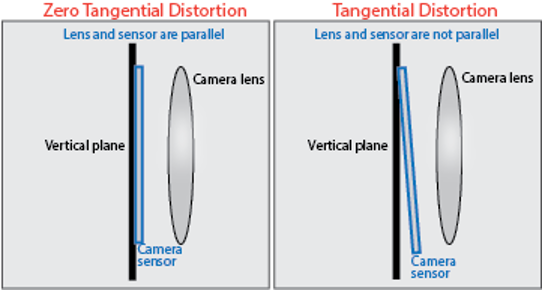
Abbildung 5: Tangentiale Verzerrung [Image Source: pho1-22-Zhang-calibration.pptx ]

Mathematische Modelle zur Korrektur fügen dem intrinsischen Kalibrierungsprozess typischerweise zusätzliche Terme hinzu, um diese Verzerrungen zu berücksichtigen.

Anwendungen der Kameraprojektion

1. 3D-Rekonstruktion: Wiedergewinnung der 3D-Geometrie einer Szene aus 2D-Bildern.
2. Robotische Bildverarbeitung: Ermöglicht die Wahrnehmung, Navigation und Interaktion von Robotern mit ihrer Umgebung.
3. Augmented Reality: Überlagerung digitaler Inhalte mit der physischen Welt.
4. Autonome Fahrzeuge: Steuerung von Fahrzeugen mithilfe präziser kamerabasierter 3D-zu-2D-Wahrnehmung und Kartierung zur Hinderniserkennung und Navigation.

e-con Systems: Ein Pionier in der Bereitstellung von OEM-Kameralösungen

e-con Systems entwickelt, konstruiert und fertigt seit 2003 OEM cameras Wir bieten hochmoderne Kameralösungen an, darunter MIPI-Kameramodule, GMSL-Kameras, USB-3.1-Gen-1-Kameras, Stereokameras,ToF-Kameras, und mehr. Im Laufe der Zeit haben wir dazu beigetragen, die Art und Weise zu verändern, wie Branchen Embedded Vision einsetzen. Dazu zählen unter anderem Einzelhandel, Medizin- und Lebenswissenschaften, Industrie, Landwirtschaft, Smart Cities und weitere Bereiche.

Nutzen Sie unseren Kamera-Selektor, um unser vollständiges Produktportfolio kennenzulernen.

Wie immer gilt: Wenn Sie Unterstützung bei der Integration von Kameralösungen in Ihre Embedded-Vision-Systeme benötigen, schreiben Sie bitte an camerasolutions@e-consystems.com.