画像処理やマッピングの分野では、3次元世界を２次元表現へ変換するために、数学的なモデル、座標変換、そしてキャリブレーションプロセスが用いられます。これらは、カメラ投影や内部・外部パラメータの理解、ならびに高精度なキャリブレーション技術によって支えられています。こうした原理の理解は、カメラキャリブレーションのみならず、自動運転車、ロボティクス、などの応用分野においても極めて重要です。
本ブログでは、カメラ投影の数学的基礎から実践的な応用例までを体系的に解説し、これらの概念を深く理解するための専門的な知見を提供します。
3次元から2次元へ：カメラ投影の概念
カメラ投影とは、現実世界の3次元空間に存在する点を、2次元の画像平面上に写像するプロセスを指します。この変換は一般にピンホールカメラモデルを用いて表現されます。ピンホールカメラモデルでは、カメラを、光が通過する単一の開口部（ピンホール）を持つ理想的な装置として近似します。
このプロセスは次の式で要約されます。
x=P.X
ここで：
-
- x：画像平面上の2次元ピクセル座標
- P：カメラ投影行列（内部パラメータおよび外部パラメータを含む行列）
- X：同次座標での3次元の世界座標
この変換プロセスは、主に次の二つの要素から構成されます。
- 外部変換：3次元点に対して回転および並進を適用することで、カメラとシーンとの相対的な位置関係を定義します。
- 内部変換：カメラの内部プロパティを用いて、変換された点を2次元の画像平面上にマッピングします。
カメラモデリングにおける座標系
3次元点が2次元表現へ変換される過程では、複数の座標系を順に経由します。これらの座標系は、それぞれ異なる役割を担っています。
- ワールド座標系：3次元シーンを定義するためのグローバルな参照フレームです。
- カメラ座標系：カメラを原点とし、シーンをカメラに対して変換します。
- 画像平面座標系：カメラが3次元点を投影してシーンを捉える2次元平面を指します。
- ピクセル座標系：デジタル画像を離散的なピクセル値で表現し、画像平面座標を実際のピクセルにマッピングします。
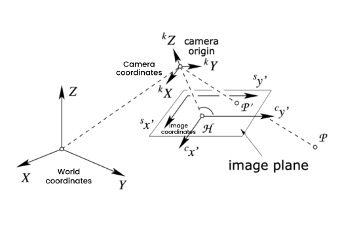図1：座標系
これらの座標系間の変換は、外部パラメータおよび 内部パラメータによって規定されます。
カメラ投影の構成要素
内部パラメータ：カメラの内部プロパティの定義
内部パラメータは、カメラの内部特性を記述するもので、カメラ座標系における3次元点を画像平面上の2次元座標へどのように投影するかを規定します。主に次の要素から構成されます。
- 焦点距離（fx、fy）：レンズからイメージセンサーまでの距離を表し、画像上での投影スケールを決定します。
- 主点（Cx,Cy）：カメラの光軸が画像平面と交差する点であります。
- アスペクト比とスキュー（s）：画像軸間の直交性のずれを補正します。
- 歪み補正パラメータ：樽型歪みや糸巻き型歪みなど、レンズの歪みを補正するためのパラメータです。
これらの内部パラメータは、次のような内部行列 にまとめて表現されます。
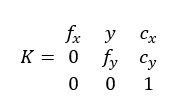
外部パラメータ：空間におけるカメラの位置と姿勢
これらのパラメータは、カメラの相対的な位置と向きを定義します。基本的には以下のとおりです。
- 回転行列 (R): カメラの姿勢を表す 3×3 の直交行列で、カメラ座標系への回転を記述します。
- 変換行列(t)：原点からカメラの位置を示す 3×1 の並進ベクトルです。
これらは通常、次のように結合されます。
[R|t]
これらのパラメータにより、カメラを3次元環境にシームレスに統合することが可能になります。これにより、3次元環境を2次元画像へマッピングする処理が完了します。
図2：チェッカーボード – ポイント検出 [画像出典：pho1-22-Zhang-calibration.pptx]
カメラキャリブレーション：投影行列の推定
カメラキャリブレーションは、3次元空間から2次元画像への正確なマッピングを実現するために、内部パラメータおよび外部パラメータを推定・決定するための処理です。
内部キャリブレーション
内部キャリブレーションでは、焦点距離、主点位置、レンズ歪みといったカメラの内部パラメータを推定することに重点を置きます。一般的には、チェッカーボードなどの幾何構造が既知のパターンを複数の視点から撮影し、Zhang の手法をはじめとするキャリブレーションアルゴリズムを用いてカメラ行列および歪みパラメータを算出します。
外部キャリブレーション
外部キャリブレーションの目的は、シーンの座標系に対するカメラの位置および姿勢（回転と並進）を推定することです。既知の3次元点と、それらに対応する画像上の2次元投影点との対応関係を用いることで、外部パラメータを導出します。
直接線形変換（DLT）
DLT法は、カメラキャリブレーションにおいて最も重要な手法の一つであり、実世界座標と画像座標との対応関係を利用します。この手法では、各対応関係から方程式系を構築し、QR分解などの線形代数的手法を用いて射影行列を推定します。
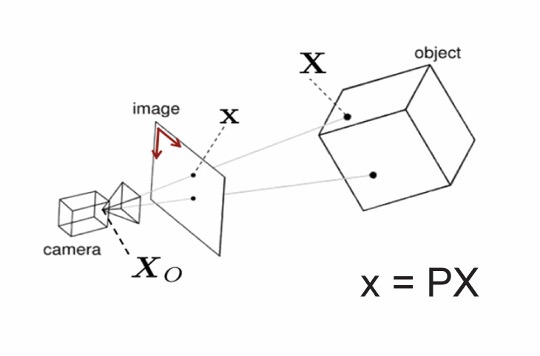
図3：直接線形変換 [画像出典：pho1-22-Zhang-calibration.pptx ]
ピンホールカメラモデルの役割
ピンホールカメラモデルは、レンズ歪みを無視し、理想的な光学系を仮定することで、投影過程を単純化したモデルです。このモデルは理想化されたものですが、投影の数学的原理を理解するための基礎となります。
このモデルでは、次のような前提が置かれます。
- 光線はすべて一点（ピンホール、すなわち光学中心）に集まり、そこを通過して像面に到達する。
- 得られる画像は上下左右が反転した像となり、その拡大・縮小の度合いは焦点距離によって決定される。
実用的な応用においては、歪み補正を導入することで、本モデルを拡張することが多く行われています。
レンズの歪みとその補正
現実には完全に理想的なレンズは存在せず、レンズ歪みは画像の幾何的精度に大きな影響を与えます。代表的な歪みの種類として、以下が挙げられます。
- 放射状歪み：画像中心からの距離に応じて発生する歪みで、本来直線であるはずの線が曲がって見えます。
- 樽型歪み：直線が画像中心から外側に向かって膨らむように湾曲します。
- 糸巻き型歪み：直線が画像中心に向かって引き込まれるように湾曲します。
図4：レンズ歪みの種類とその補正方法
- 接線方向の歪み：レンズのずれによって発生し、画像が非対称にずれる原因となります。
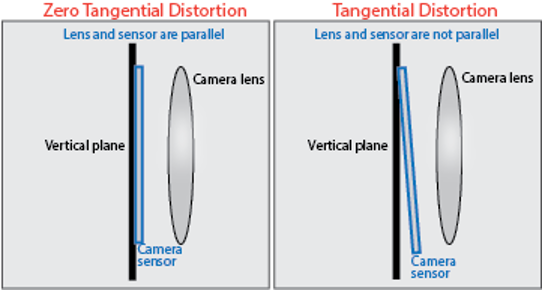
図5：接線方向歪み [画像出典：pho1-22-Zhang-calibration.pptx ]
歪み補正のための数理モデルでは、レンズ歪みの影響を考慮するために、キャリブレーションモデルに追加の補正項を追加するのが一般的です。
カメラ投影の応用例
- 3D再構成：複数の2次元画像からシーンの3次元形状や構造を復元する技術です。
- ロボットビジョン：ロボットが周囲の環境を認識し、自己位置推定、ナビゲーション、物体操作などを行うための視覚技術です。
- 拡張現実：実世界の映像にデジタルコンテンツを重ね合わせ、現実と仮想を融合させる技術です。
- 自動運転車：高精度なカメラベースの 3D–2D 認識およびマッピングを活用し、車両の誘導、障害物検知、環境理解、ナビゲーションを実現します。
e-con Systems：OEMカメラソリューションを提供するパイオニア企業
e-con Systems は、2003 年以来、OEM 向けカメラ の設計・開発・製造を手がけてきた企業です。 MIPI カメラモジュール, GMSL カメラ, USB 3.1 Gen 1 カメラ, ステレオカメラ,ToF カメラなど, 最先端のカメラソリューションを幅広く提供しています。これまでに、リテール、医療・ライフサイエンス、産業、農業、スマートシティなど、さまざまな分野における組み込みビジョンシステムの発展を支援してきました。
製品ラインナップの詳細については、当社の カメラセレクター をご利用ください。
また、組み込みビジョンシステムへのカメラソリューションの統合に関するご相談やサポートが必要な場合は、camerasolutions@e-consystems.comまでお気軽にお問い合わせください。
Prabu Kumarは、e-con Systemsの最高技術責任者兼カメラ製品責任者であり、組み込みビジョン分野で15年以上の豊富な経験があります。彼は、USBカメラ、組み込みビジョンカメラ、ビジョンアルゴリズム、FPGAに関する深い知識をも有しています。医療、工業、農業、小売、生体認証などのさまざまなドメインにまたがる50以上のカメラソリューションを構築してきました。また、デバイスドライバー開発とBSP開発の専門家でもあります。現在は、新時代のAIベースのアプリケーションを強化するスマートカメラソリューションの構築に全力を注いでいます。