Objektivdatenblätter enthalten oft Informationen zur Verzerrung, die Fotografen und Ingenieuren helfen sollen, das Verhalten des Objektivs zu verstehen. Objektivverzerrung bezeichnet das Phänomen, dass gerade Linien in einer Szene im endgültigen Bild gekrümmt erscheinen. Dies liegt daran, dass Objektive das Licht nicht aus allen Teilen des Sichtfelds perfekt fokussieren.
In diesem Blog analysieren wir die Verzerrungsparameter in Objektivdatenblättern und die drei Möglichkeiten, wie die Verzerrung dargestellt wird.
Arten der Linsenverzerrung
Es gibt drei Hauptarten von Linsenverzerrungen, die in der Fotografie häufig auftreten:
- Tonnenförmige Verzerrung: Dadurch werden gerade Linien nach außen gebogen, ähnlich der Wölbung eines Fasses. Dies kommt häufig bei Weitwinkelobjektiven vor.
- Kissenförmige Verzeichnung: Gerade Linien werden nach innen gebogen, ähnlich wie bei einem Nadelkissen. Diese Verzerrung tritt häufiger bei Teleobjektiven auf.
- Schnurrbartverzerrung (Wellenformverzerrung): Dies ist eine weniger häufige Verzerrung, bei der gerade Linien wellenförmig erscheinen, wie bei einem Schnurrbart.
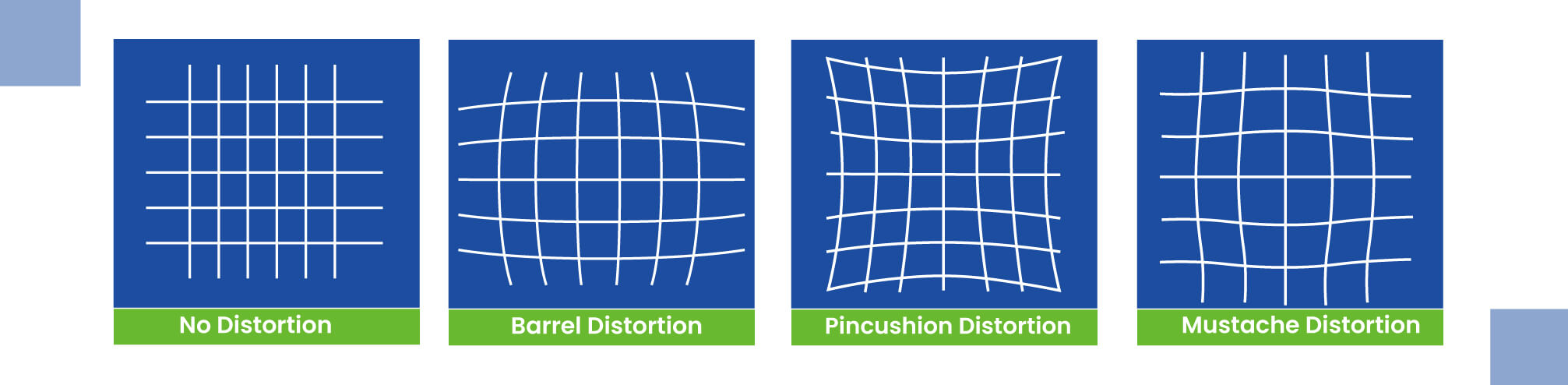
Hier ist eine Visualisierung zum besseren Verständnis, um die oben genannten Verzerrungen besser unterscheiden zu können:
Stellen Sie s eine Szene mit einem quadratischen Raster vor. Bei einer tonnenförmigen Verzerrung wölbt sich das Raster nach außen, wodurch die Quadrate an den Rändern breiter erscheinen. Bei einer kissenförmigen Verzerrung sinkt das Raster nach innen, wodurch die Quadrate an den Rändern schmaler erscheinen. Bei einer Schnurrbartverzerrung werden die Rasterlinien wellig.
Mathematische Darstellung der Verzerrung auf drei Arten
Mathematisch gesehen kann die Verzerrung im Datenblatt eines Objektivs auf drei verschiedene Arten dargestellt werden. Sehen wir uns diese im Detail an.
1. Optisch/Rectilinear/F-Tan (Theta)
Die optische Verzerrung stellt den Gesamtverzerrungsparameter des optischen Systems dar. F-Tan Theta oder die optische Verzerrung kann mit der folgenden Formel berechnet werden.
F-Tan (Theta)-Verzerrung = (Realbildhöhe – Referenzbildhöhe/Referenzbildhöhe) *100
War,
Referenzbildhöhe (mm) = Brennweite (mm) X Tan (halbes Maximales DFOV in Grad)
Beispiel: Berechnen wir die tonnenförmige Verzerrung mit der oben angegebenen Formel der Halbwinkelmethode.
- Maße erfassen:
Effektive Brennweite (F): 4,4 mm (Abstand vom optischen Zentrum des Objektivs zum Bildsensor)Diagonales Sichtfeld (FOV) bei einer bestimmten Bildentfernung: Werte, die bei unterschiedlichen Bildentfernungen angegeben werden (z. B. 124° bei 10 mm)
Bilddiagonale: 10 mm (Diagonale des Bildsensors)
- Berechnen Sie die Referenzhöhe:
Dies stellt die ideale Höhe dar, die ein Objekt hätte, wenn es keine Verzerrung gäbe.Halbdiagonales Sichtfeld: Teilen Sie das diagonale Sichtfeld durch 2 (z. B. 124° / 2 = 62°).
Referenzhöhe = F * tan (halbes diagonales Sichtfeld): (4,4 mm * tan (62°)) = 8,27519 mm
- Verzerrungsprozentsatz berechnen:
Reale Höhe: Die Hälfte der diagonalen Abmessung des Bildes (in diesem Fall 5 mm)Verzerrung % = ((Realhöhe – Referenzhöhe) / Referenzhöhe) * 100 %Dadurch wird die prozentuale Differenz zwischen der tatsächlichen Objekthöhe und der idealen Höhe aufgrund der Verzerrung berechnet.
Ein negativer Wert deutet auf eine tonnenförmige Verzeichnung hin (Objekte erscheinen an den Rändern kleiner). Im obigen Beispiel zeigt die Berechnung eine höhere tonnenförmige Verzeichnung (-39,5 %) bei einem größeren Bildabstand (10 mm). Mit abnehmendem Bildabstand (9 mm und 5 mm) werden die Verzerrungsprozentsätze weniger negativ, was auf eine Verringerung des tonnenförmigen Effekts hindeutet.
Die F*tan(Theta)-Methode ist ein allgemeinerer Ansatz zur Berechnung der Verzeichnung. Sie wird häufig zur ersten Beurteilung der Verzeichnung bei verschiedenen Objektiven, einschließlich Fotoobjektiven, verwendet. Diese Methode hilft zu verstehen, wie gerade Linien aufgrund von Verzeichnung von ihrer idealen Position abweichen.
F*tan(Theta)-Berechnungen werden bei Kamerakalibrierungsprozessen eingesetzt, um Verzerrungsparameter zur Korrektur aufgenommener Bilder abzuschätzen. Objektivdesigner nutzen F*tan(Theta)-Berechnungen häufig während der Designphase, um die Verzerrung im fertigen Objektiv vorherzusagen und zu minimieren. Dies trägt zur Entwicklung von Objektiven mit minimaler Bildkrümmung bei und gewährleistet eine präzise Bildwiedergabe.
2. F(Theta)
Die F(Theta)-Methode konzentriert sich auf die Winkelbeziehung zwischen dem idealen unverzerrten Bildpunkt und dem tatsächlich verzerrten Bildpunkt, ohne dass Vergrößerungsinformationen erforderlich sind.
Schritte zum Berechnen der F-Theta-Verzerrung mit F*Theta (Radiant):
- Wandeln Sie die Hälfte des diagonalen Sichtfelds (Theta/2) von Grad in Radiant um (multiplizieren Sie mit Pi/180).
- Multiplizieren Sie die Brennweite (F) mit dem Winkel im Bogenmaß, um die Referenzhöhe zu erhalten (ideale, unverzerrte Bildhöhe basierend auf der Winkelposition).
- Vergleichen Sie die tatsächliche Bildhöhe mit der Referenzhöhe, um den Verzerrungsprozentsatz zu berechnen.
F-Theta-Objektive sind speziell dafür ausgelegt, eine konstante Bildgröße (bzw. Punktgröße bei Lasern) über ein Scanfeld hinweg aufrechtzuerhalten.Die F-Theta-Berechnung hilft, die Genauigkeit dieser konstanten Größe zu gewährleisten, indem Abweichungen vom Ideal gemessen werden. . Diese Objektive werden in verschiedenen Anwendungen wie Lasermarkierung und -gravur, Laserschneiden, 3D-Druck und LiDAR eingesetzt.
Die F-Tan(Theta)-Methode verwendet die Tangensfunktion, um den Winkel mit der Objektgröße und der Vergrößerung in Beziehung zu setzen. Die F(Theta)-Methode hingegen konzentriert sich auf die Winkelposition des Bildpunkts relativ zum Mittelpunkt. Beide Methoden erfordern die Brennweite (F) und das diagonale Sichtfeld (Grad). Bei der F(Theta)-Methode wird das Sichtfeld in Grad jedoch in Radiant umgerechnet.
Die F-Tan (Theta)-Methode verwendet die tan(theta)-Beziehung, um eine Referenzhöhe basierend auf der Vergrößerung zu berechnen, und die F(Theta)-Methode verwendet F*Theta (Radiant), um die ideale Bildpunktposition basierend auf ihrer Winkelposition darzustellen.
Beide Methoden können zur Abschätzung der Verzerrung verwendet werden, sind aber in bestimmten Situationen besser geeignet. F-Tan (Theta) wird bevorzugt, wenn der Fokus auf der Objektgröße liegt und sich die Vergrößerung aufgrund der Verzerrung ändert. Die F(Theta)-Methode wird verwendet, um die Winkelbeziehung verzerrter Bildpunkte zu ermitteln, ohne dass Vergrößerungsinformationen erforderlich sind.
3. TV-Verzerrung
Die TV-Verzerrung stammt, wie der Name schon sagt, aus dem Fernsehbereich. Sie lässt sich mit der folgenden Formel berechnen:
TV-Verzerrung (Tonnenförmig) = ((Referenzbildhöhe – Realbildhöhe)/(Realbildhöhe)] x 100 )/2
Die oben angegebene Formel bezieht sich auf die Verzerrung bei halbem Sichtfeld.
Die oben angegebene Formel berechnet die tonnenförmige Verzeichnung auf der Grundlage mehrerer Faktoren:
- Abmessungen des Bildsensors: Für die Berechnung werden die halbe Diagonale und die halbe Vertikale des Bildsensors verwendet.
- Optische Verzerrungswerte: Diese Werte stellen den Grad der Verzerrung dar, ausgedrückt als negativer Prozentsatz für die tonnenförmige Verzerrung. Die Formel verwendet separate Verzerrungswerte für das diagonale Sichtfeld (DFOV) und das vertikale Sichtfeld (VFOV) des Objektivs.
- Kosinus des diagonalen Sichtfelds (cos (DFOV)): Dieser mathematische Begriff bezieht den Winkel des diagonalen Sichtfelds in die Berechnung ein.
Die Formel berechnet die Differenz zwischen der erwarteten Höhe eines Objekts basierend auf der Sensorgröße und seiner tatsächlichen verzerrten Höhe basierend auf den Verzerrungswerten und dem Sichtfeld. Diese Differenz wird dann als Prozentsatz der vertikalen Sensorgröße ausgedrückt, um ein Maß für die tonnenförmige Verzerrung zu liefern.
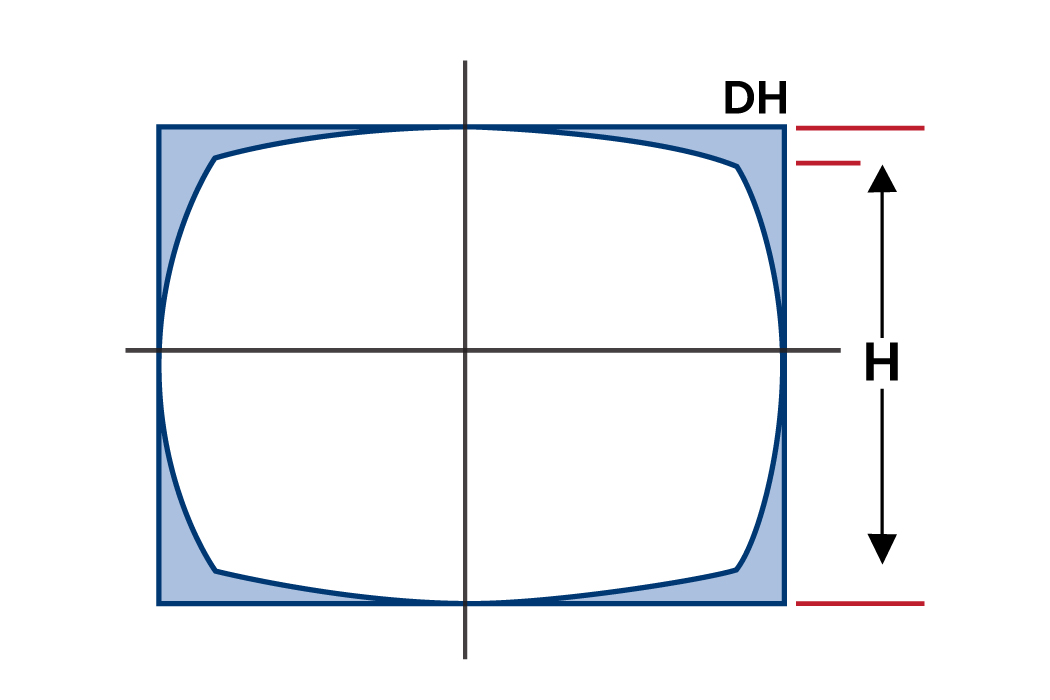
Abbildung 1: TV-Verzerrung – Tonnenförmig
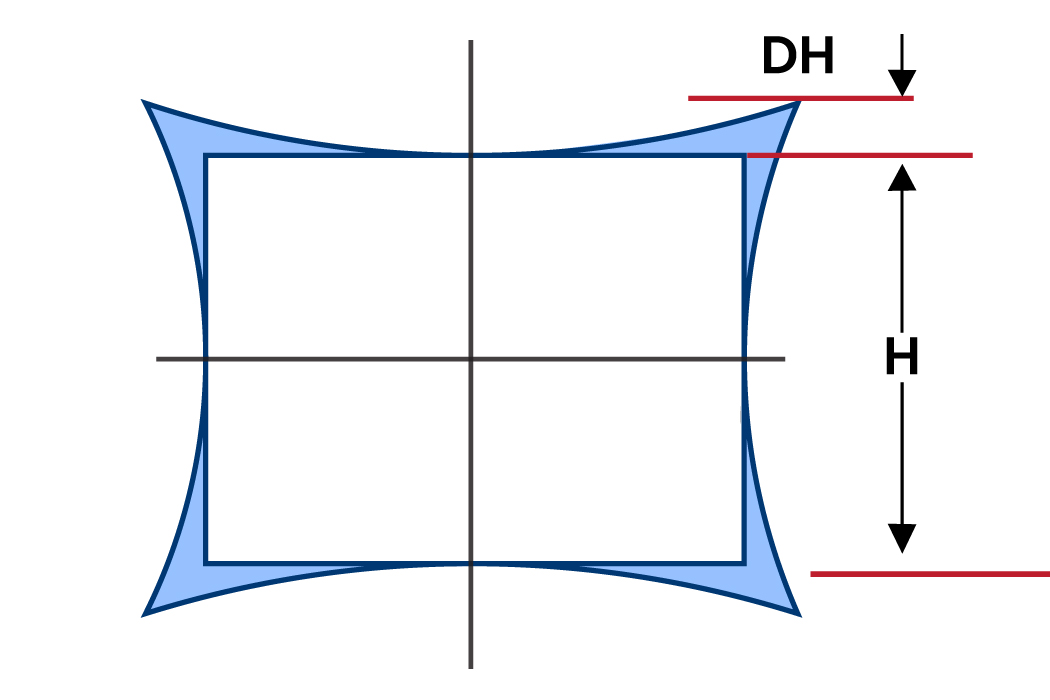
Abbildung 2: TV-Verzerrung – Kissenverzerrung
Entdecken Sie die OEM-Kameras von e-con Systems, die für Ihre Embedded Vision-Anwendung geeignet sind
e-con Systems ist ein Branchenpionier mit über 20 Jahren Erfahrung im Design, der Entwicklung und Herstellung von OEM-Kameras .
Wir kennen die Kameraanforderungen von Embedded Vision-Anwendungen und bauen unsere Kameras so, dass sie den Anforderungen der Branche optimal entsprechen.
Wir bieten außerdem verschiedene Anpassungsdienste an , darunter Kameragehäuse, Auflösung, Bildrate und Sensoren Ihrer Wahl, um sicherzustellen, dass unsere Kameras perfekt in Ihre Embedded Vision-Anwendungen passen.
Besuchen Sie die e-con Systems Kameraauswahlseite, um unser breites Angebot an Kameras zu erkunden.
Bei Fragen senden Sie uns eine E-Mail an camerasolutions@e-consystems.com.

Prabu ist Chief Technology Officer und Head of Camera Products bei e-con Systems und verfügt über eine reiche Erfahrung von mehr als 15 Jahren im Bereich der eingebetteten Bildverarbeitung. Er bringt umfassende Kenntnisse in den Bereichen USB-Kameras, eingebettete Bildverarbeitungskameras, Bildverarbeitungsalgorithmen und FPGAs mit. Er hat über 50 Kameralösungen für verschiedene Bereiche wie Medizin, Industrie, Landwirtschaft, Einzelhandel, Biometrie und mehr entwickelt. Er verfügt außerdem über Fachwissen in der Gerätetreiberentwicklung und BSP-Entwicklung. Derzeit liegt der Schwerpunkt von Prabu auf der Entwicklung intelligenter Kameralösungen, die KI-basierte Anwendungen des neuen Zeitalters ermöglichen.