카메라 투영 및 매개변수를 이해하기 위한 종합 가이드

3D 세계를 2D 표현으로 이미징하고 매핑하는 세계에서는 수학적 모델, 변환 및 보정 프로세스에 의존합니다. 이러한 프로세스는 카메라 투영, 내재적 및 외재적 매개변수, 정확한 보정을 위한 기술과 같은 개념에 의해 주도됩니다. 이러한 원칙을 이해하는 것은 카메라 보정과 자율 주행 차량, 로봇 공학 등과 같은 응용 분야에서 매우 중요합니다.

이 블로그에서는 카메라 프로젝션의 수학적 기초와 실용적 응용을 분석하면서 이러한 개념에 대한 전문가의 통찰을 얻을 수 있습니다.

3D에서 2D로: 카메라 프로젝션의 개념

카메라 프로젝션의 핵심은 현실 세계의 3D 포인트를 2D 이미지 평면에 매핑하는 것입니다. 이러한 변환은 종종 빛이 들어오는 단일 조리개를 가진 간단한 장치로 취급하는 핀홀 카메라 모델을 사용하여 모델링됩니다.

그 과정은 다음과 같이 요약할 수 있습니다:

x=P.X

• • x: 이미지 평면의 2D 픽셀 좌표
  • P: 카메라 투영 행렬(내재적 및 외재적 매개변수 포함)
  • X: 균질한 형태의 3D 월드 좌표

이 변화에는 다음이 포함됩니다:

1. 외부 변환: 3D 포인트를 회전시키고 이동시켜 카메라를 장면에 대해 상대적으로 배치합니다.
2. 내재적 변환: 카메라의 내부 속성을 사용하여 이 변환된 점들을 2D 이미지 평면에 매핑합니다.

카메라 모델링에서의 좌표계

3D 포인트가 2D 표현으로 이동하는 과정은 여러 좌표계에 걸쳐 있습니다:

1. 세계 좌표계: 글로벌 기준 프레임을 사용하여 3D 장면을 정의합니다.
2. 카메라 좌표계: 카메라를 원점으로 배치하고, 그에 따라 세상이 변합니다.
3. 이미지 평면: 카메라가 3D 지점을 투사하여 장면을 포착하는 2D 평면이 포함됩니다.
4. 픽셀 좌표계: 디지털 이미지를 이산 픽셀 값으로 나타내며, 이미지 평면 좌표를 실제 픽셀과 연결합니다

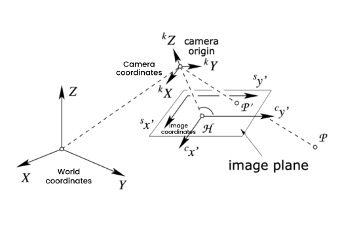
그림 1: 좌표계

이 시스템들 간의 각 변환은 내재적 및 외재적 매개변수에 의해 유도됩니다.

카메라 프로젝션의 구성 요소

내재적 매개변수: 카메라의 내부 속성 정의

내재적 매개변수는 카메라의 내부 특성을 설명하며, 카메라 공간의 3D 좌표를 이미지 평면의 2D 좌표로 변환하는 방법을 캡슐화합니다. 여기에는 다음이 포함됩니다:

• 초점 거리(fx,fy): 렌즈에서 이미지 센서까지의 거리를 나타내며, 투영의 규모를 나타냅니다.
• 주점(Cx,Cy): 광축이 교차하는 이미지 평면의 중심.
• 종횡비 및 스큐(s): 이미지 축 간의 직교성에서 벗어나는 모든 편차를 수정합니다.
• 왜곡 매개변수: 배럴 왜곡(외부로 굽힘) 또는 핀쿠션 왜곡(내부로 굽힘)과 같은 렌즈 왜곡을 해결합니다.

내재 행렬 K는 다음 매개변수들을 결합합니다: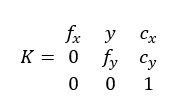

외부 매개변수: 우주에서 카메라 찾기

이러한 매개변수는 카메라의 상대적 위치와 방향을 정의합니다. 여기에는 다음이 포함됩니다:

• 회전(R): 카메라의 방향을 나타내는 3×3 직교 행렬.
• 번역(t): 카메라의 원점으로부터의 변위를 지정하는 1×3 열 벡터.

결합된 형태:
[R|t]

이러한 매개변수를 통해 카메라를 3D 환경에 원활하게 통합할 수 있습니다. 이렇게 하면 3D 세계를 2D 이미지로 매핑할 수 있습니다.

그림 2: 체커보드 – 포인트 감지 [이미지 출처: pho1-22-Zhang-calibration.pptx ]

Camera Calibration: The Projection Matrix

카메라 보정: 프로젝션 매트릭스
보정은 3D 세계에서 2D 이미지로의 정확한 매핑을 보장하기 위해 내재적 및 외재적 매개변수를 결정하는 데 도움이 됩니다.

내재적 보정
이 단계에서는 초점 거리, 주점, 렌즈 왜곡과 같은 매개변수를 결정하는 데 중점을 둡니다. 보정에는 알려진 패턴(예: 체커보드)의 이미지를 캡처하고 Zhang의 방법과 같은 알고리즘을 적용하여 카메라 매트릭스를 계산하는 것이 포함됩니다.

외부 보정
여기서 목표는 장면에서 카메라의 위치와 방향을 추정하는 것입니다. 알려진 3D 월드 포인트를 2D 투영과 일치시키면 외부 매개변수를 도출할 수 있습니다.

직접 선형 변환(DLT)
DLT 방법은 세계 지점과 이미지 지점 간의 대응 관계를 활용하여 보정의 가장 중요한 이정표입니다. 이 방법은 각 대응 관계에 대한 방정식을 공식화하고 QR 분해와 같은 선형 대수 기법을 사용하여 투영 행렬을 해결합니다.

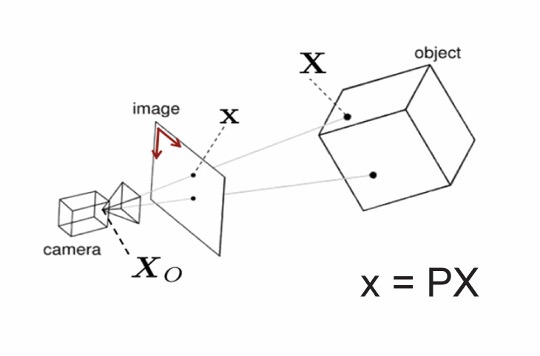그림 3: 직접 선형 변환 [이미지 출처: pho1-22-Zhang-calibration.pptx ]

핀홀 카메라 모델의 역할

핀홀 카메라 모델은 렌즈 왜곡을 무시하고 완벽한 광학을 가정하여 투영 과정을 간소화합니다. 이상적이지만 투영의 수학을 이해하는 데 기초가 됩니다.
이 모델에서는:

• 광선은 한 지점(핀홀)에서 수렴하여 이미지 평면으로 통과합니다.
• 결과 이미지는 초점 거리에 따라 스케일링이 결정되며 반전되고 스케일링됩니다.

실제 응용 프로그램은 종종 왜곡 보정을 도입하여 이 모델을 확장합니다.

렌즈 왜곡과 그 보정

완벽한 렌즈는 없으며 왜곡은 이미지 품질에 큰 영향을 미칠 수 있습니다. 일반적인 유형에는 다음이 있습니다:

1. 방사 왜곡: 직선은 곡선처럼 보입니다
   • 배럴 왜곡: 선은 중앙에서 바깥쪽으로 구부러집니다
   • 핀쿠션 왜곡: 선이 안쪽으로 구부러짐

   

   그림 4: 렌즈 왜곡 유형 및 보정

2. 접선 왜곡: 렌즈 정렬이 잘못되어 이미지가 비대칭적으로 이동하여 발생합니다.

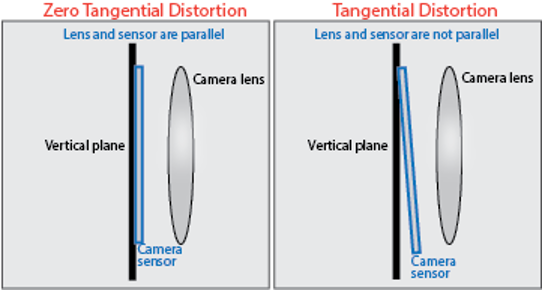
그림 5: 접선 왜곡 [이미지 출처: pho1-22-Zhang-calibration.pptx ]

수정을 위한 수학적 모델은 일반적으로 이러한 왜곡을 설명하기 위해 내재적 보정 과정에 용어를 추가합니다.

카메라 프로젝션의 응용

1. 3D 재구성: 2D 이미지에서 장면의 3D 지오메트리 복원.
2. 로봇 비전: 로봇 인식, 내비게이션 및 환경과의 상호 작용을 가능하게 합니다.
3. 증강 현실: 디지털 콘텐츠를 물리적 세계에 오버레이하기.
4. 자율 주행 차량: 정확한 카메라 기반 3D-to-2D 인식과 장애물 감지 및 내비게이션을 위한 매핑을 사용하여 차량을 안내합니다.

e-con 시스템: OEM 카메라 솔루션 제공의 선구자

e-con Systems는 2003년부터 OEM 카메라를 설계, 개발 및 제조해 왔습니다. 저희는MIPI 카메라 모듈, GMSL 카메라, USB 3.1 1세대 카메라, 스테레오 카메라,ToF 카메라, 등 최첨단 카메라 솔루션을 제공합니다. 시간이 지남에 따라 업계가 임베디드 비전에 접근하는 방식을 변화시키는 데 도움을 주었습니다. 여기에는 소매, 의료 및 생명 과학, 산업, 농업, 스마트 시티 등이 포함됩니다.

카메라 셀렉터를 사용하여 전체 제품 포트폴리오를 확인하세요.

항상 그렇듯이, 내장된 비전 시스템에 카메라 솔루션을 통합하는 데 도움이 필요하시면, camerasolutions@e-consystems.com에 문의 주시기 바랍니다.